Square Root

In this article we are going to discuss all about square root.

Square of a Positive Integer

Before learning about square root you have to know about square of a positive integer.

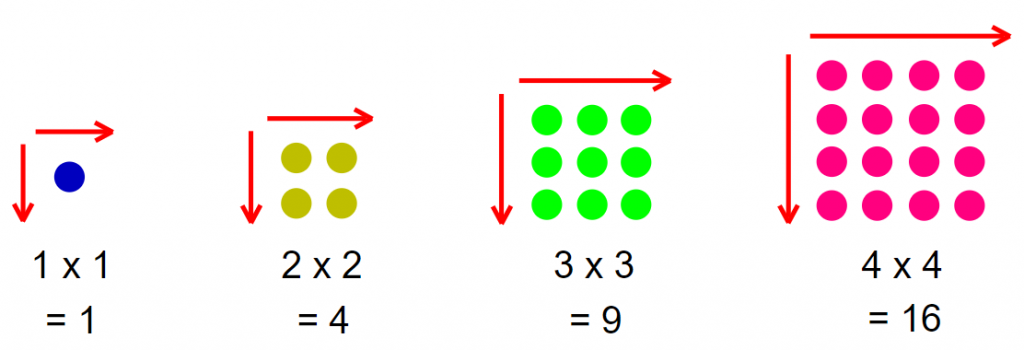
The numbers such as 1, 4, 9, 16, … which can be represented by using dot patterns to get a square shape are called Square Numbers.

The number that we obtain by multiplying a number by itself is called the Square of that number.

Example:

4 x 4 = 16
16 is the square of 4.

Square of a Negative Integer

Square of a negative integer is also obtained by multiplying the negative integer by itself.

Let’s find the square of (-4)

(- 4) x (- 4)
= 16

Here, when we multiply (-) x (-) it gives (+) and 4 x 4 = 16

That is the reason for the answer to be +16 or just 16.

Let’s discuss another example.

Find the square of (-7).

(-7) x (-7)
= 49

Square of any negative integer will always be a positive value.

What is Square Root?

Before move in to the definition lets try to understand the concept by looking at a real life scenario.

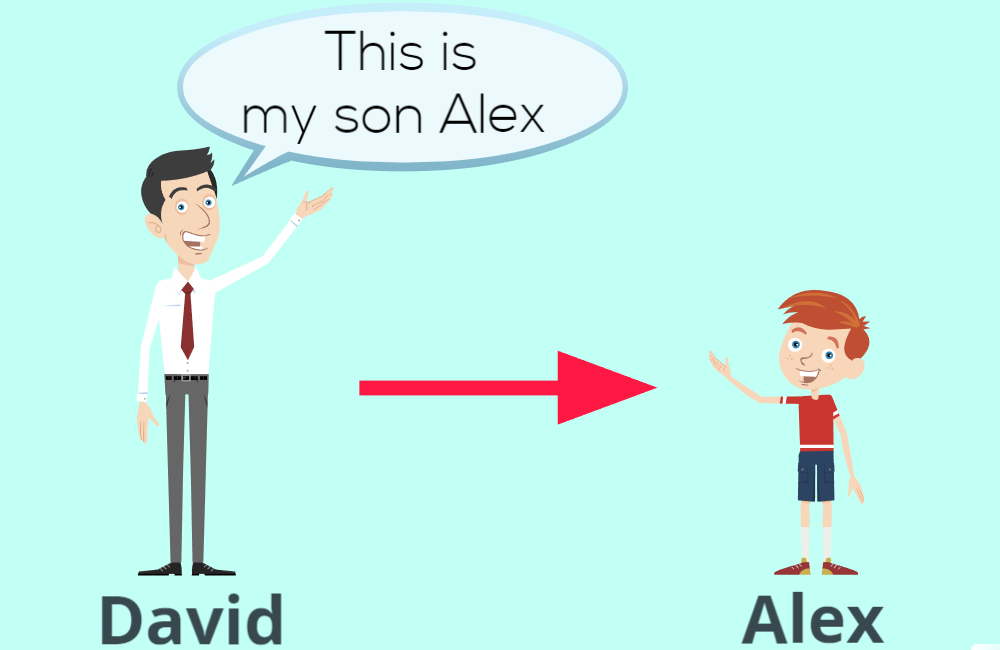
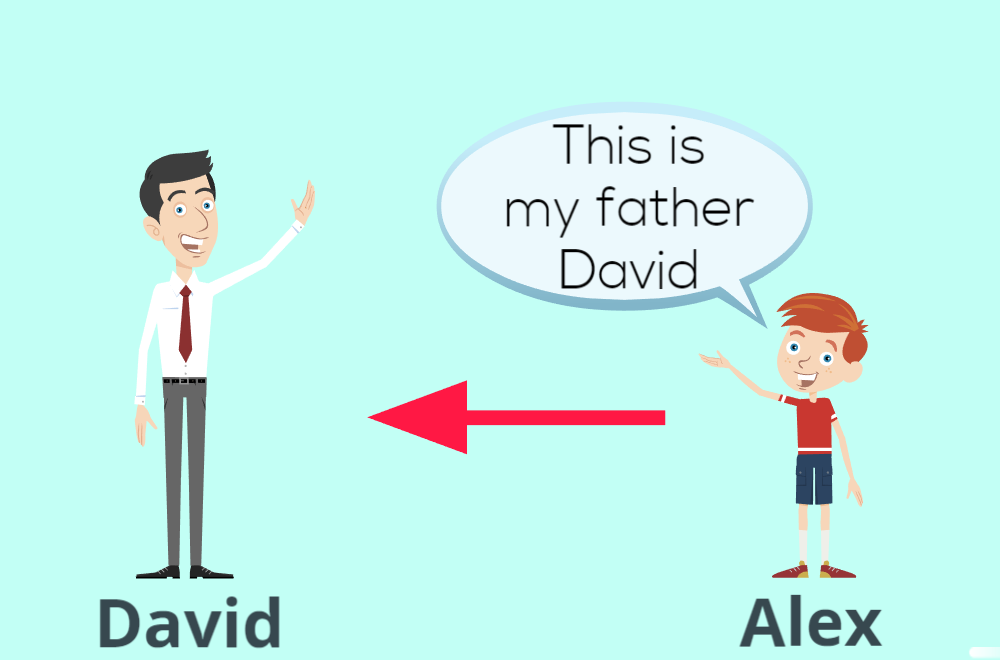
By looking at the above situation I think you can understand relationship and also the difference.

When David (the father) introduce Alex, he use the phrase “This is my son Alex”

When Alex (the son) introduce David he use the phrase “This is my father David”

The relationship between Square and Square Root is somewhat similar to the above situation.

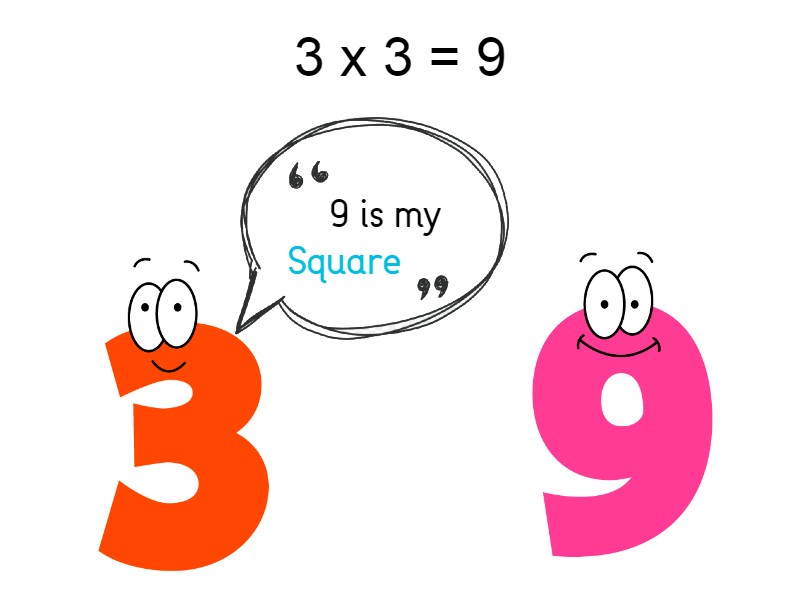
When we consider about sq. root of 9,

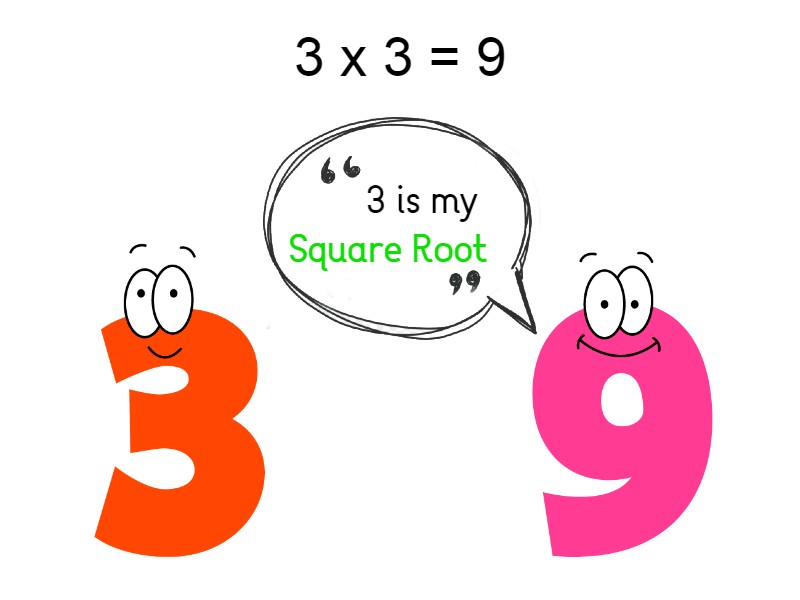
9 is a perfect square. Sq. root of 9 is 3.

When we take the square root of a perfect square it will always give a whole number.

If a number is the square of another number, then the second number is the square root of the first number.

Square Root Symbol

To indicate the sq. root of a number we use the symbol given below.

To express square root of 9, we write it as

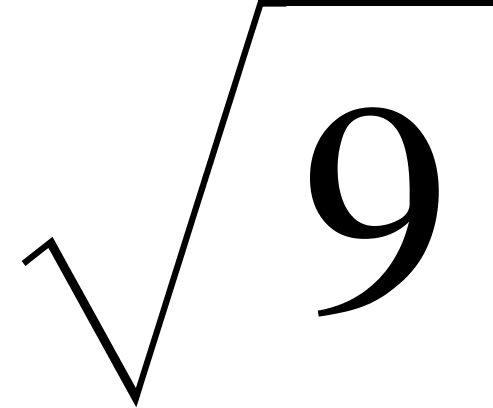
And we know that,

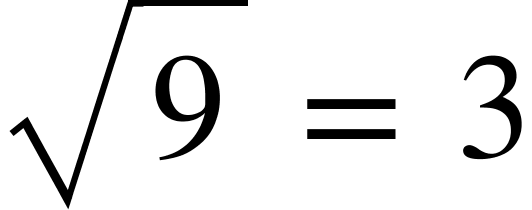
Same as above,

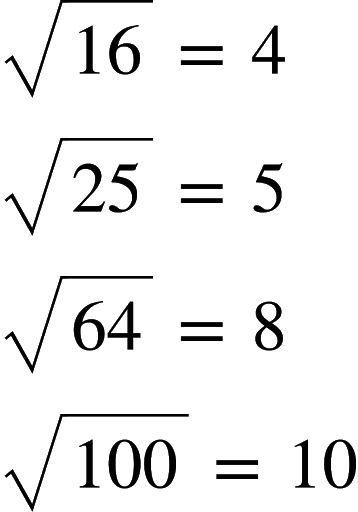
What is Perfect Square?

The square of a positive integer is called a Perfect Square.

Perfect Squares Up to 1000

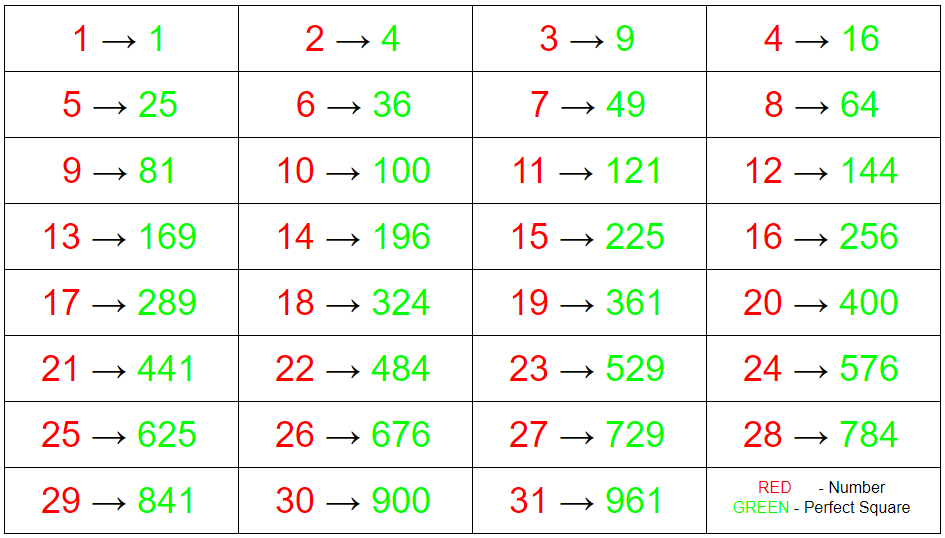
Digits in the Units Place of a Perfect Square

This is a special property in perfect square numbers. By looking at the digit in the ones place we can get an idea of whether it is possible to be a square number or not.

In our previous subtopic, we found perfect square numbers up to 1000. By looking at them we can see that the digits in the units place of a perfect square is one of the digits 0, 1, 4, 5, 6, or 9.

And also we can see that none of the digits 2, 3, 7 and 8 are not on the ones place of on a perfect square.

Example:

Is 2467 a perfect square?
No. This can’t be a perfect square. Because the digit in the ones place is 7.

---

There are several methods to find sq. root. In this article let’s talk about two easy methods.

Methods to Find Square Root

01. By Using Prime Factors

Let’s discuss this method through examples.

Example 01:

Find the square root of 144.

First you have to divide 144 by its prime factors as follows.

144 = 2 x 2 x 2 x 2 x 3 x 3

Now separate above factors into two groups equally.

144 = ( 2 x 2 x 3 ) x ( 2 x 2 x 3 )
By using index notation we can express,
144 = ( 2 x 2 x 3 )²

Therefore

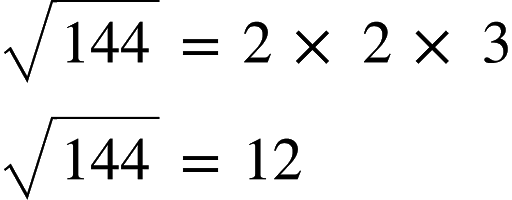
Example 02:

Find the square root of 324.

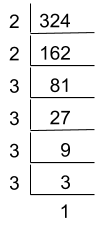
324 = 2 x 2 x 3 x 3 x 3 x 3 x 3
324 = ( 2 x 3 x 3 ) x ( 2 x 3 x 3 )
= ( 2 x 3 x 3 )²

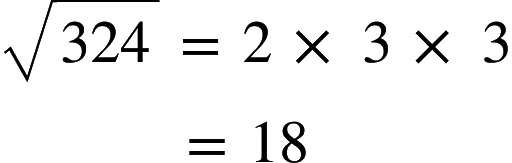
Exercise:

The area of a square-shaped land is 256 m². Find the length of a side of the land.

---

02. By observation

Previously we discussed the digit in the ones place of perfect squares. As you can remember I am going to summarize that one in another way.

Digit in the ones place of the perfect square	Digit in the ones place of the square root
1	1 or 9
4	2 or 8
5	5
6	4 or 6
9	3 or 7
0	0

Example 01:

We know that 64 is a perfect square.

8 x 8 = 64

Then when we consider sq. root of 64, it is,

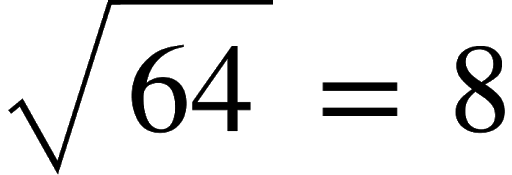
The digit in the ones place of the perfect square is 64 is 4.

According to the above table,ones place digit of the square root should be 2 or 8. As you can see it is 8.

From now on we are going to use this table to find square root.

Example 02:

Find the square root of 784.

This is a three-digit number. So you have to consider the digit in the hundreds place to find the digit in the tens place of the sq. root.

Let’s follow the steps in order.

First check the digit in the ones place. It is 4.

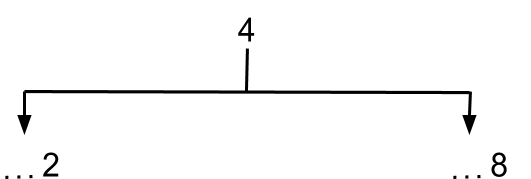
So the digit in the ones place of the sq. root will be 2 or 8.

Now let’s find the digit in the tens place of the sq. root.

For that, we have to consider the hundreds place digit which is 7.
Now we have to find sq. root of perfect squares close to 7 and less than 7.
Perfect square closer to 7 and less than 7 is 4 and sq. root of 4 is 2.

So the digit for the blank will be 2. That makes the sq. root of 784 is 22 or 28.

To check the correct answer you have to multiply them and see.

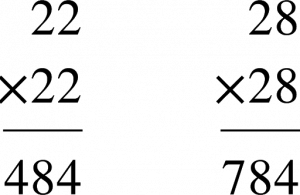
Accordingly

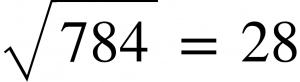
I think this lesson is clear to you. Try to do more exercises and build up your speed.

I hope to discuss about multiplying sq. root from another article.

FAQ