Let’s learn LCM – Least Common Multiple, HCF – Highest Common Factor in this lesson.
Before we move into the LCM and HCF, we have to know about ,
-
Factors
-
Prime Factors
-
Multiples
What are the Factors?
If a number is divisible by another number without a remainder that the second number is a factor of the first number.
Example:
8 is divisible by 2 without any remainder.
∴ 2 is a factor of 8.
How to find Factors?
There are a few methods. Let’s discuss through an example.
Example:
Find all the factors of 36.
Express 36 as a product of two whole numbers
36 = 1 x 36
36 = 2 x 18
36 = 3 x 12
36 = 4 x 9
36 = 6 x 6
When a 36 written as a product of two whole numbers, those two numbers can be called a factor of 36.
Factors of 36 are,
1 , 2 , 3 , 4 , 6 , 9 , 12 , 18 and 36
FACT:
0 is not a factor of any whole number.
Also, you can find factors using divisibility rules.
What are Prime Factors?
Numbers with exactly two distinct factors are called Prime Numbers.
In other words,
A number only divisible by 1 and the same number itself is the prime number.
Prime numbers among factors of a number are Prime Factors.
Example:
Prime factors of 36 are,
2 and 3
What are Multiples?
A number that obtained by multiplying the given whole number by any whole number is a Multiple.
Example:
Find four multiples of 3.
3 x 1 = 3
3 x 2 = 6
3 x 10 = 30
3 x 15 = 45
So, 3, 6, 30 and 45 are multiples of 3.
Now we are done with basics. Let’s move into our Lesson – LCM
LCM – Least Common Multiple
The meaning of LCM is the Least Common Multiple, also known as the lowest common multiple. That means we are going to find common multiples between two or more numbers and finally select the smallest multiple from them.
We have 3 methods to find the LCM.
Find LCM – Method 01
In this method, we list out a few multiples of given numbers in ascending order and select the least common multiple among them.
Example:
LCM of 3, 4, 6
Multiples of 3 : 3, 6, 9, 12, 18, 21, 24, 27, 30, 33, 36, 39, …
Multiples of 4 : 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, …
Multiples of 6 : 6, 12, 18, 24, 30, 36, 42, 48, 54, …
Now you can see 12, 24 and 36 are some common multiples between 3, 4 and 6.
We want the least one. So the LCM is 12.
Find LCM – Method 02
For this method, we use knowledge about prime factors.
Example :
Let’s do the same example which is finding LCM of 3, 4 and 6
Write each number as a product of its prime factors.
Hint: Divide the numbers by their prime factor as follows.
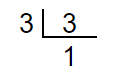
3 = 3
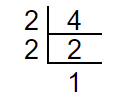
4 = 2 x 2
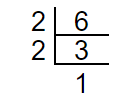
6 = 2 x 3
3 = 3 = 31
4 = 2 x 2 = 22
6 = 2 x 3 = 21 x 31
Select the greatest power of each prime factor.
There are two distinct prime factors which are 2 and 3.
The greatest power of 2 = 22
The greatest power of 3 = 31
The LCM is given by the product of these greatest powers.
= 22 x 31
= 2 x 2 x 3
= 12
So the LCM is 12.
Find LCM – Method 03
In this method divide until you get 1 in last raw.
Example:
Find the LCM of 4, 12, 18
01. Write the numbers as follows
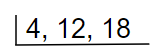
02. Use only prime factors and continue division.
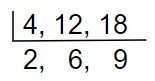
We can divide 2 and 6 by 2 but not 9.
No problem with that just continue.

When you have 1s in these rows don’t divide them. Just carry the value downwards.
03. Now we have 1s in the last raw, the division is done.
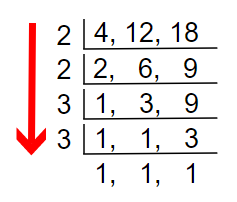
Take the product and it will be your LCM.
LCM of 4, 8, 18 is = 2 x 2 x 3 x 3
= 36
HCF / GCD – Highest Common Factor / Greatest Common Factor
Now let’s move on to HCF / GCD
The meaning of HCF is Highest Common Factor.
That means we are going to find the largest factor among the common factors of a few numbers.
For this one also we have 3 methods.
Find HCF – Method 01
List out all the factors of given numbers and select the largest one among them.
Example:
Find the HCF of 24, 16, 48
Factors of 24 : 1, 2, 3, 4, 6, 8, 12, 24
Factors of 16 : 1, 2, 4, 8, 16
Factors of 48 : 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Common factors are, 2, 4 and 8
So the HCF is 8
Find HCF – Method 02
Let’s discuss this method directly through an example.
Example:
Find the HCF of 72 and 90

72 = 2 x 2 x 2 x 3 x 3
90 = 2 x 3 x 3 x 5
Select the common factors and take their product.
HCF = 2 X 3 X 3
= 18
So the HCF of 72 and 90 is 18
Find HCF – Method 03
In this method also we use division. But in this method, we can only divide if we have a common prime factor for given numbers.
Let’s do the same example
Example:
Find the HCF of 72 and 90

Here in 2nd step, we cannot divide both by 2.
We have to stop our division because there are isn’t any prime number which divides both 4 and 5.
HCF = Product of the factors
= 2 x 3 x 3
= 18
In this article, you learnt three methods to find LCM and three methods to find HCF (GCD). Practice any method you like. Try some problems. You can use our LCM and GCD Calculator to check your answers.
LCM, HCF (GCD / GCF) Calculator
If LCM Calculator not loads or you need to calculate LCM/ HCF of three numbers, please click here.
FAQ
What is LCM?
LCM – Least Common Multiple, also known as the lowest common multiple. In LCM, finding common multiples between two or more numbers and finally select the smallest multiple from them.
What is HCF?
HCF – Highest Common Factor, also known as Greatest Common Divisor(GCD). In HCF, finding the largest factor among the common factors of a few numbers.
What are the Factors?
If a number is divisible by another number without a remainder that the second number is a factor of the first number.
What are Prime Factors?
Numbers with exactly two distinct factors are called Prime Numbers. In other words,A number only divisible by 1 and the same number itself is the prime number.
What are Multiples?
A number that obtained by multiplying the given whole number by any whole number is a Multiple.


Pingback: LCM HCF Calculator | Free Math Tools | Math Tutor
Pingback: Square Root | Introduction | Examples and Exercises | Math Tutor
Pingback: Matrices | Learn All About Matrix with Examples | Math Tutor