Similarity,
In what follows, we’ll see that many—if not most—of our results shall rely on the proportionality of sides in similar triangles. A convenient statement is as follows.
Similarity, Given the similar triangles ΔABC ∼ ΔA’BC’,
We have that,
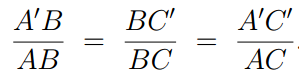
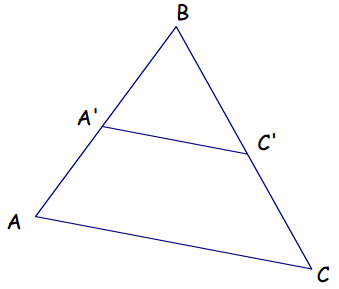
Conversely, if
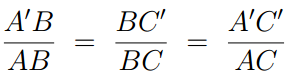
then triangles ΔABC ∼ ΔA’BC’ are similar.
Proof
Note first that ΔAA’C’ and ΔCA’C’ clearly have the same areas, which implies that ΔABC’ and ΔCA’B have the same area (being the previous common area plus the area of the common triangle ΔA’BC’).
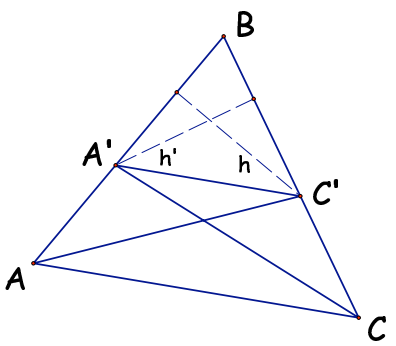
Therefore,
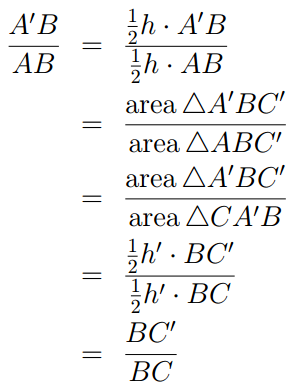
In an entirely similar fashion, one can prove that
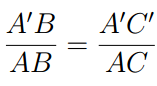
Conversely, assume that
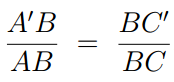
In the figure below, point C” has been located so that the segment [A’C”] is parallel to [AC]. But then triangles ΔABC and ΔA’BC” are similar,
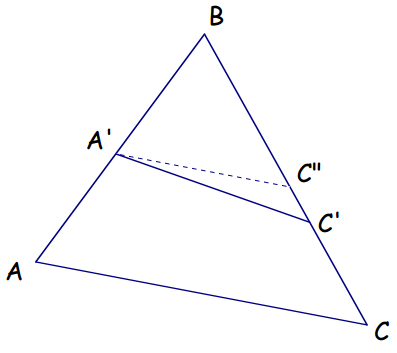
and so,
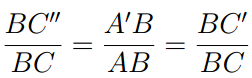
i.e. that BC” = BC’ . This clearly implies that C’ = C”, and so [A’C’ ] is parallel to [AC]. From this, it immediately follows that triangles Δ ABC and ΔA’BC’ are similar.
Exercises for Similarity
01. Let ΔABC and ΔA’B’C’ be given with ABC = A’B’C’ and
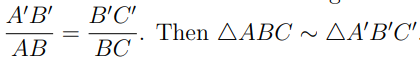
02.
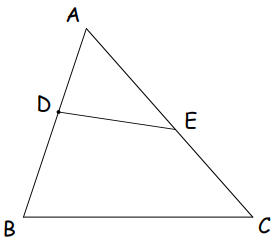
In the figure to the right, AD = rAB, AE = sAC.
Show that
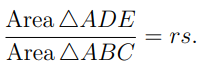
03. Let ΔABC be a given triangle and let Y, Z be the midpoints of [AC], [AB], respectively. Show that (XY ) is parallel with (AB). (This simple result is sometimes called the Midpoint Theorem)
04.
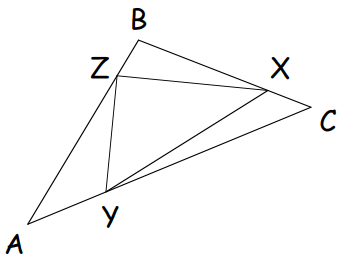
In ΔABC, you are given that
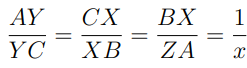
where x is a positive real number. Assuming that the area of ΔABC is 1, compute the area of ΔXYZ as a function of x.
05. Let ABCD be a quadrilateral and let EF GH be the quadrilateral formed by connecting the midpoints of the sides of ABCD. Prove that EF GH is a parallelogram.
06.
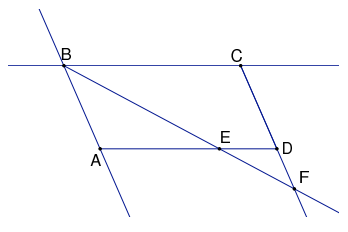
In the figure to the right, ABCD is a parallelogram, and E is a point on the segment [AD]. The point F is the intersection of lines (BE) and (CD). Prove that AB × FB = CF × BE.
07.
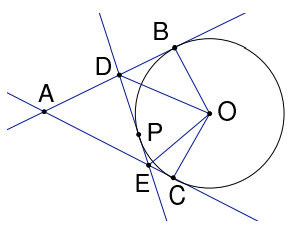
In the figure to the correct, tangents to the circle at B and C meet at point A. P is found on the minor arc BC and the tangent to the circle at P meets the lines (AB) and (AC) at the points D and E, respectively. Prove that DOE = ½BOC, where O is that the center of the circle.
Related Lessons: Pythagorean theorem

