The Pythagorean Theorem

Right-angled triangle and the Pythagorean theorem

In this article lets try to develop the Pythagorean theorem by means of the right angle.

So first let’s get some proper ideas about the right-angled triangle.

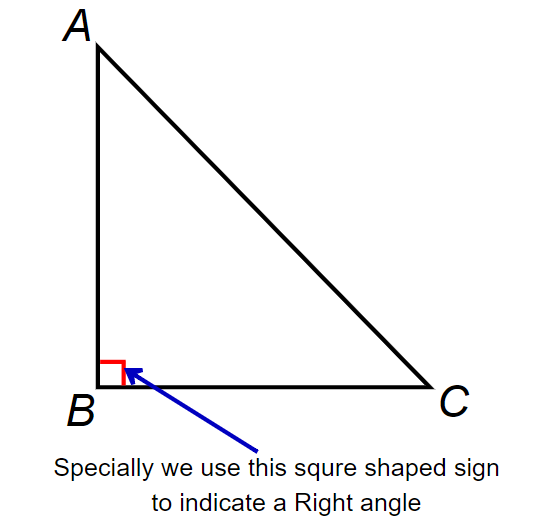
What is a right-angled triangle?

If an angle of a triangle is 90^o it is called a right-angled triangle or right triangle.

Special Right Triangles

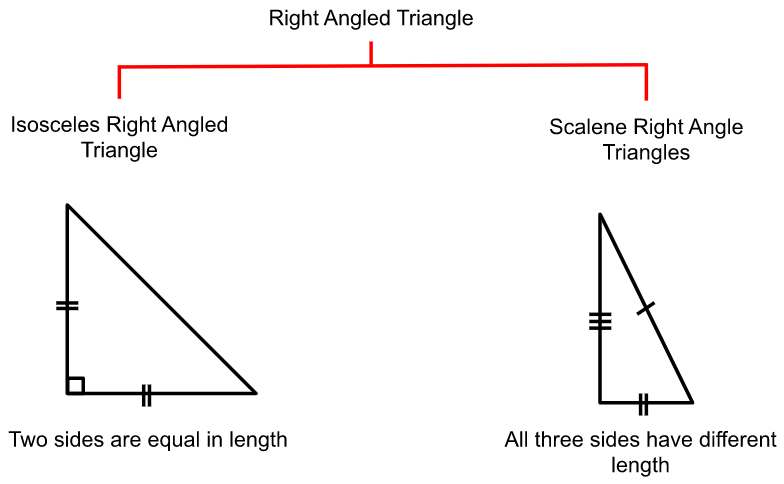
Classification of right triangles according to their sides

Classification of right triangles according to their Angles

Other than the above two types of right-angled triangles there are two main right-angled triangles that you always search for.

30 60 90 Triangle

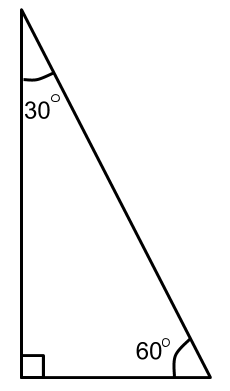
This is actually a Scalene Right Angled Triangle.

45 45 90 Triangle

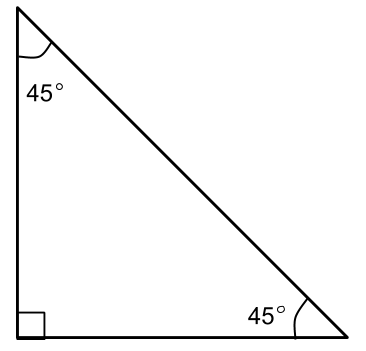
This is an Isosceles triangle.

Terms Related to Right Angled Triangle

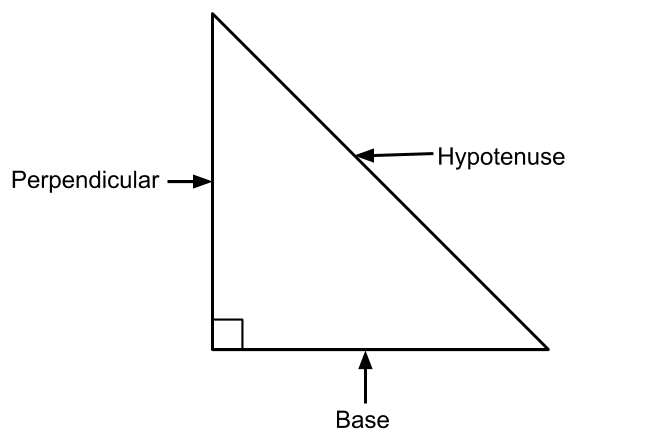
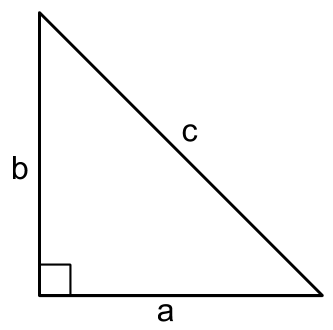
The side which is opposite to the right angle and which is the longest side of the triangle is called Hypotenuse.

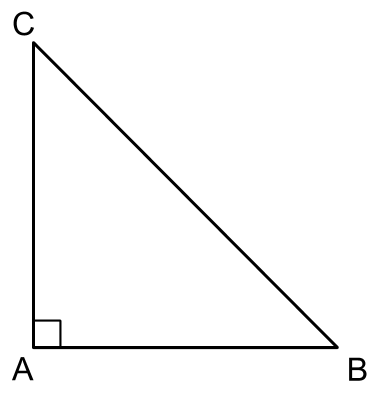
BC = Hypotenuse
AB / AC = Base
AB / AC = Perpendicular

The sides AB and AC are also called the sides which include the right angle.

The Pythagorean Theorem

This is also called as Pythagoras’ theorem or Pythagorean relationship. This is a fundamental relation in euclidean geometry.

There are several methods to prove the Pythagorean theorem. In this article, I’m going to discuss two methods.

The Pythagorean Theorem Proof – Method 01

Let’s build the proof through an example.

Draw a right-angled triangle ABC where AB = 4 cm, AC = 3 cm and BC = 5 cm

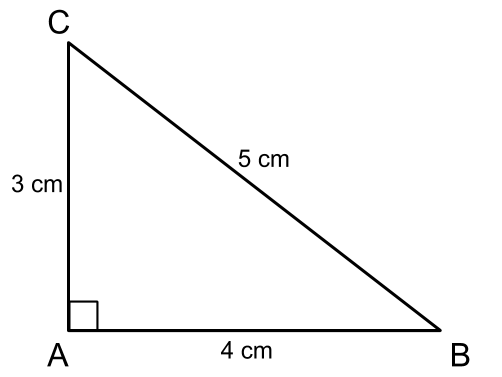
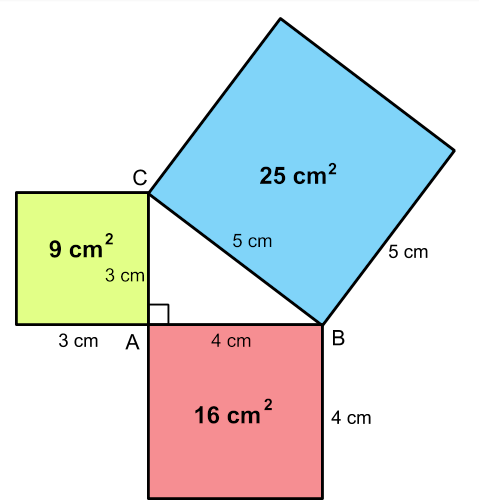
By looking at the figure we can see that,

Area of the square on BC = Area of the square on AB + Area of the square on AC

25 = 16 + 9
= 25

Accordingly

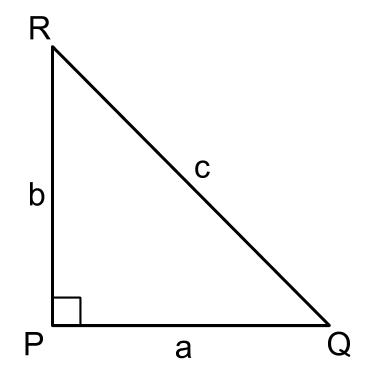
Area of the square drawn on PQ = a²
Area of the square drawn on PR = b²
Area of the square drawn on QR = c²

Therefore,

c² = a² + b²

This is called the Pythagorean theorem.

The Pythagorean Theorem Proof – Method 02

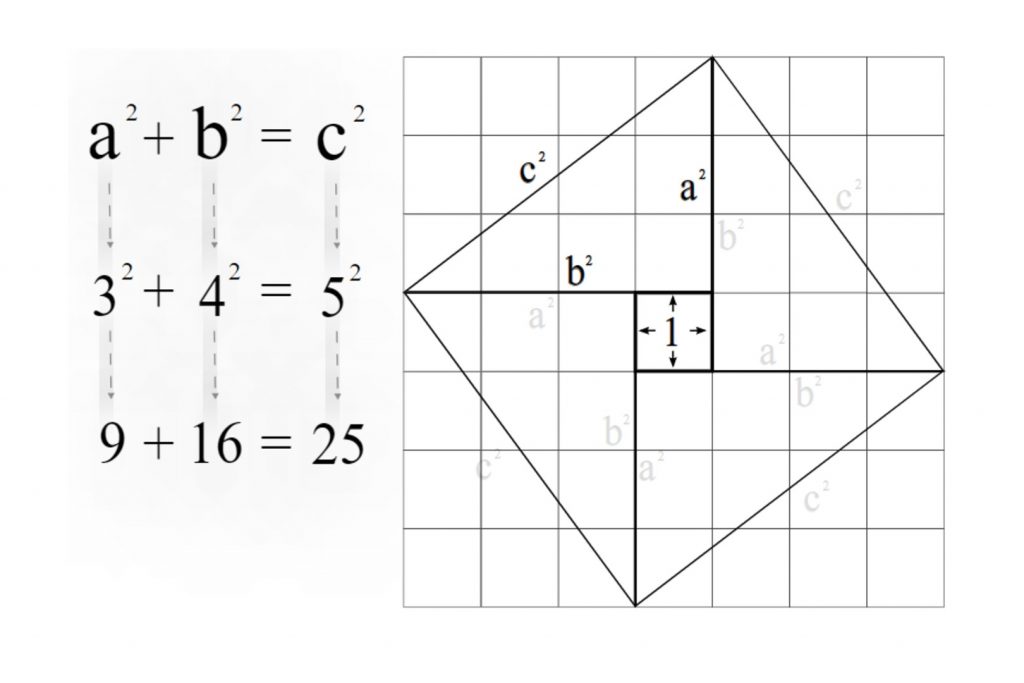
The figure to the proper indicates one among the various known proofs of this fundamental result. Indeed, the area of the “big” square is (a + b)² and can be decomposed into the area of the smaller square plus the areas of the four congruent triangles.

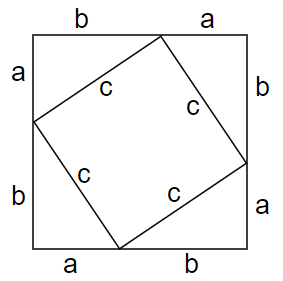
That is,

(a + b)² = c² + 2ab

which immediately reduces to a² + b² = c²

Pythagorean Triples

Pythagorean Triples are three positive integer values which satisfy the Pythagoras theorem c² = a² + b²

Below table includes few Pythagorean triples examples.

a2	b2	c2
3	4	5
6	8	10
7	24	25
5	12	13
20	21	29
8	15	17
20	99	101
48	55	73
17	144	145
9	40	41
11	60	61
12	35	37
13	84	85
16	63	65
28	45	53
33	56	65
36	77	85
39	80	89
48	55	73
65	72	97

Pythagorean Theorem Calculator

---

Exercises:

01.

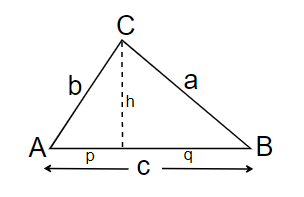
Prove Euclid’s Theorem for Proportional Segments, i.e., given the right triangle ΔABC as indicated, then
h² = pq, a² = pc, b² = qc

02. Prove that the sum of the interior angles of a quadrilateral ABCD is 360^◦.

03.

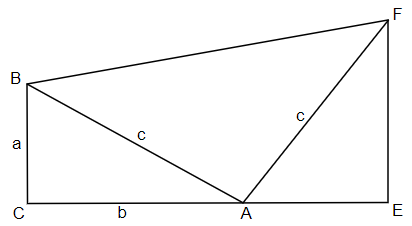
In the diagram to the right, ΔABC is a right triangle, segments [AB] and [AF] are perpendicular and equal in length, and [EF] is perpendicular to [CE]. Set a = BC, b = AB, c = AB, and deduce President Garfield’s proof* of the Pythagorean theorem by computing the area of the trapezoid BCEF.

---

*James Abram Garfield (1831–1881) published this proof in 1876 in the Journal of Education (Volume 3 Issue 161). While a member of the House of Representatives. He was assassinated in 1881 by Charles Julius Guiteau. As an aside, notice that Garfield’s diagram also provides a simple proof of the fact that perpendicular lines in the planes have slopes which are negative reciprocals.

Related lessons: Trigonometric Identities

FAQ about Pythagorean Theorem