In this article, we are going to discuss how to convert Mixed Numbers to Improper Fractions.
Before moving into that part, let’s recall what mixed numbers and improper fractions are.
A whole pizza and exactly half of an identical pizza shown in the figure. Therefore the total amount of pizza in the picture is 1 + ½
It writes as 1 ½
A number which is the sum of a whole number and a proper fraction written in this manner defined as Mixed Numbers
Examples:
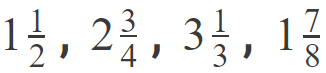
Do you know that there is a significant relationship between improper fractions and mixed numbers?
Let’s learn about improper fractions and also about the relationship between these two through an example.
I want to divide three Apples with the same size equally between Ann and David.
Case 01
So each one will get an apple and half of another apple the amount can represent as 1½
Case 02
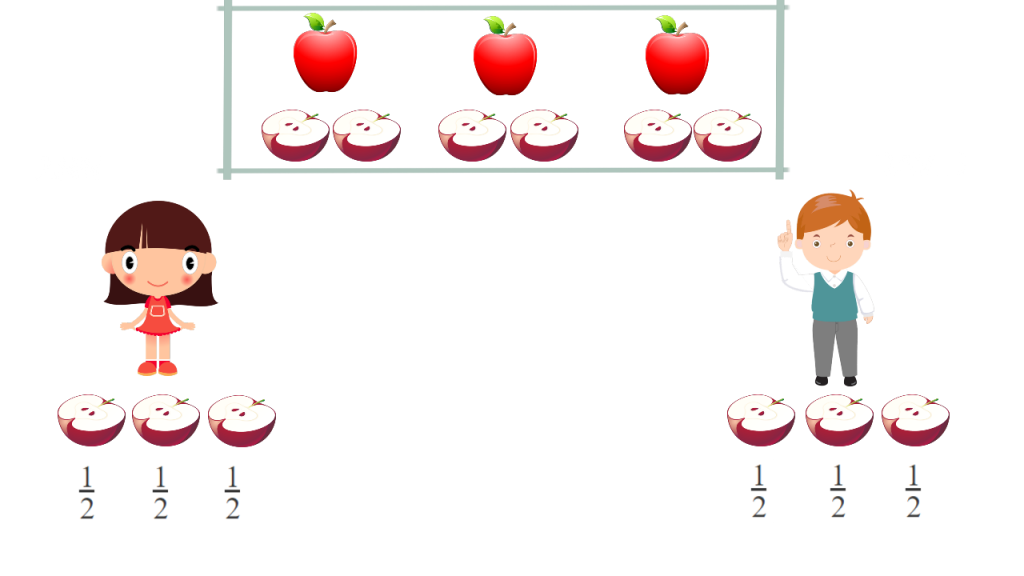
By looking at the figure you can see, the amount each child receives can show as
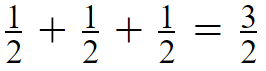
You can refer to the article on how to Addition of Fractions here.
It will be apparent to you that in both of the above cases, each child receives the same amount of apple.
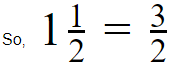
In the fraction 3/2 the numerator is greater than the denominator
If the numerator is greater than or equal to the denominator, it defines as an Improper Fraction.
Examples:
Now let’s move to our lesson, which is conversions between Mixed Numbers and Improper Fractions.
Representing a Mixed Number as an Improper Fraction
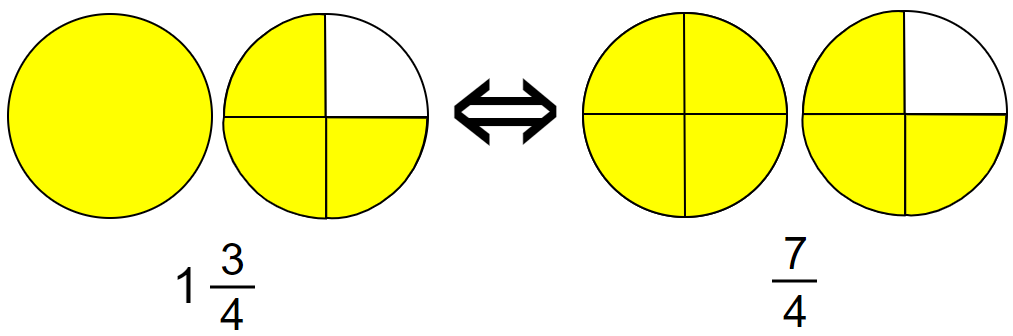
Let’s try to describe the shaded region.
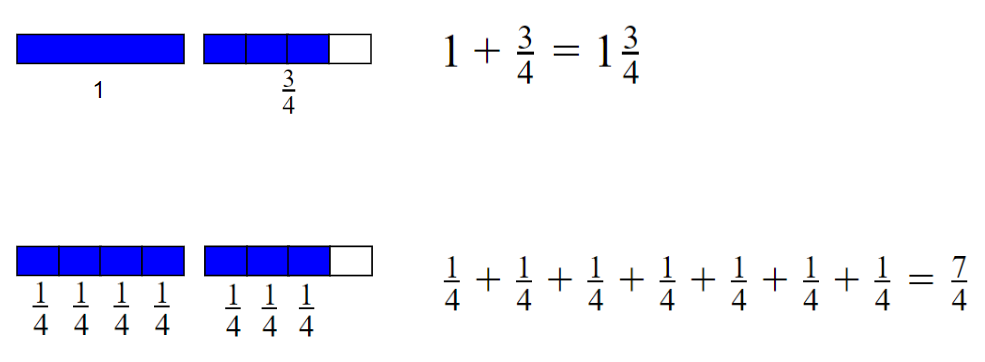
By looking at the above figures, you can see
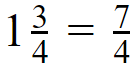
There are two methods to convert the mixed number into an improper fraction.
Let’s discuss the same example in two methods.
Method 01
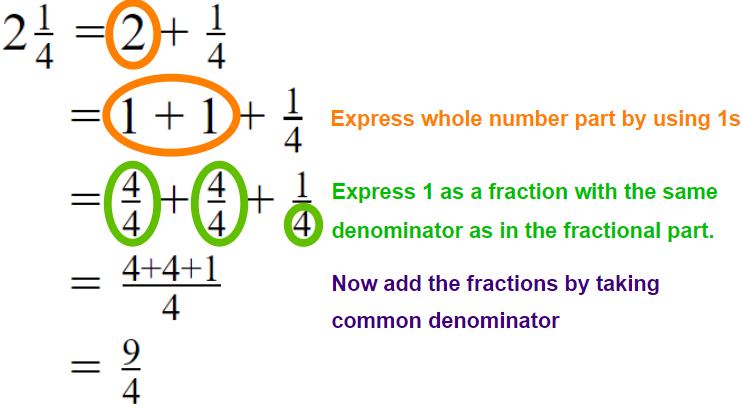
Method 02
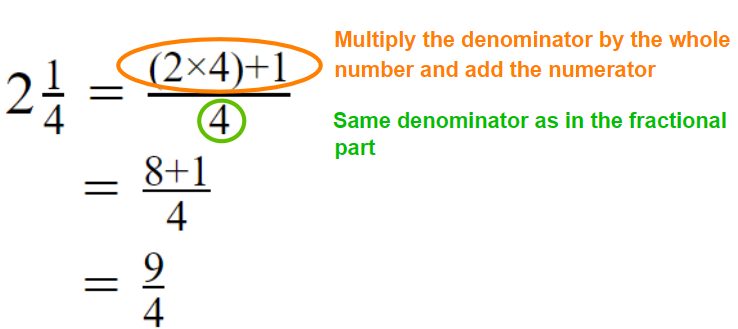
Representing an Improper Fraction as a Mixed Number
Let’s find the shaded region in the figure by using two methods
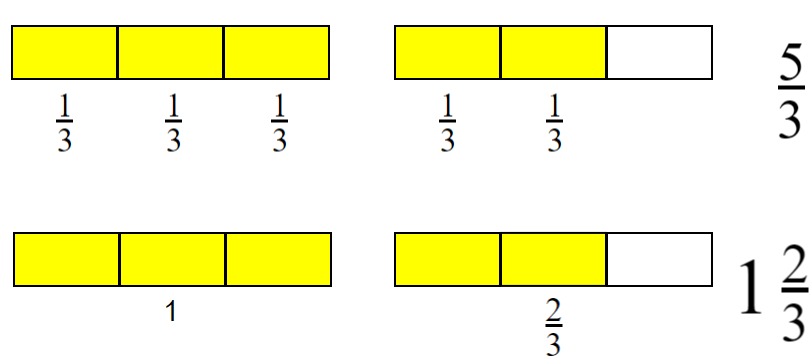
We have two ways to convert these fractions.
Let’s discuss the same example in two methods.
Method 01
Method 02
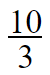
In this method, we have to use long division. Divide the numerator by denominator.
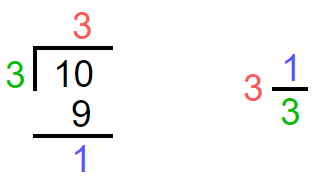
Let’s discuss another example.
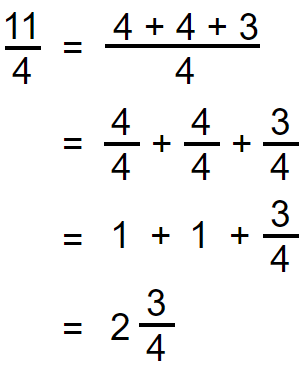
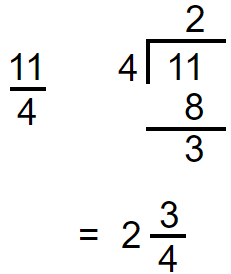
Pingback: Addition of Fractions | Math Tutor