
How to Multiply Fractions
Multiply fractions can discuss under three main categories.
- Multiplication of proper fractions
- Multiplication of improper fractions
- Multiplication of a mixed numbers
Multiplication of Proper Fractions
A proper fraction is a fraction that is less than one, with the numerator less than the denominator.
Example :
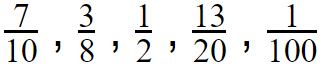
To multiply proper fractions you have to follow only three simple steps
Step 1 – Multiply the numerators
Step 2 – Multiply the denominators
Step 3 – Simply the fraction to it’s the simplest form (You have to follow this step, only when we have common factors for the numerator and denominator. Otherwise keep it as it is. )
Now let’s discuss a few simple examples
Example 01 :
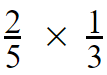
Now let’s solve this one by following the above three simple steps.
Step 01 and Step 02 ( if it is difficult for you to multiply you can use a multiplication table )

Step 03 –
By following step 01 and step 02 we got our answer as
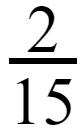
In step 03, we have to simplify the fraction. But in the above answer, we can see that there are no common factors (a number which divides both 2 and 15).
So the final answer will be,
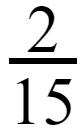
Example 02 :
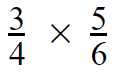
Step 01 and Step 02
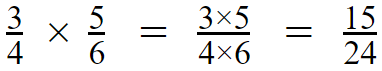
Now we got
as our answer. We can see that both 15 and 24 can
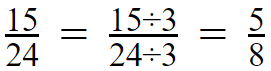
The final answer will be,
Example 03 :
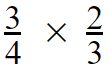
Step 01 and Step 02
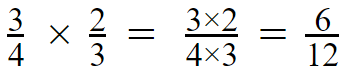
Step 03 –
For this numerator and denominator, we have several common factors such as 2,3 and 6.
out of those factors you have to select the greatest common factor (and also called as the Highest Common Factor – HCF)
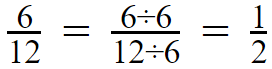
So the final answer will be
Think that you cannot find the greatest common factor,
which is 6 in the above example. Don’t get confused. You can continue to simplify the fraction with any common factor that you remember.
Let’s think that you could only find 2 as a common factor. Just continue with 2.
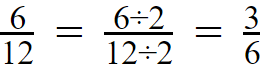
In our new fraction which is
again, we can see that 3 is a common factor.
Multiplication of Improper Fractions
An Improper Fraction is a fraction in which the numerator is greater than the denominator
Example:
To multiply improper fractions you have to follow only three simple steps
Step 1 – Multiply the numerators
Step 2 – Multiply the denominators
Step 3 – Convert the improper fraction into a mixed number
Now let’s discuss a few simple examples
Example 1 :
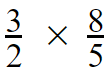
Step 01 and Step 02
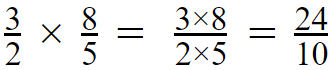
Step 03 –
We cannot keep the answer as an improper fraction, so we have to convert it into a mixed number. There are several methods to do the conversion.
Let me explain an easy method for you.
In this method, You have to use the long division. Divide the numerator by denominator.
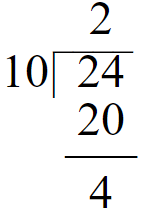
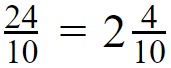
So the final answer is
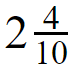
Example 02 :
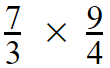
Step 01 and Step 02
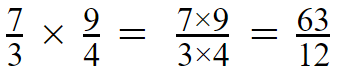
Step 03 –
Divide 63 by 12, Then the quotient is 5 and the remainder is 3.
The answer is
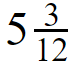
Multiplication of a Mixed Numbers
A number which is the sum of a whole number and a proper fraction written in this manner defined as Mixed Numbers
Examples :
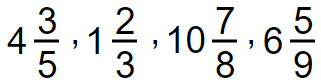
To multiply mixed numbers you have to follow four simple steps
Step 1 – Convert the mixed number into improper fraction
Step 2 – Multiply the numerators
Step 3 – Multiply the denominators
Step 4 – Express the answer as a mixed number
Example 01 :

Step 01
Write each mixed number as an improper fraction.
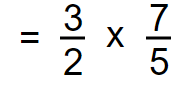
Step 02 and Step 03
Multiply numerator by numerator and denominator by denominator
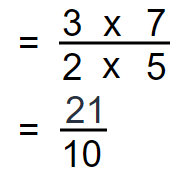
Step 04
Convert the improper fraction to mixed number
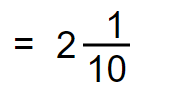
Example 02 :
You can remove the common factors as follows.

Example 03 :

Now you have knowledge of how to multiply fractions. Also you have to practice,
- how to multiply mixed fractions with different denominators
- how to multiply fractions by fractions
- how to divide and multiply fractions
- how to multiply two fractions
If you have any difficult point about how to multiply two fractions, please leave a comment below.
Exercise 01
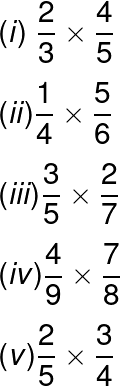
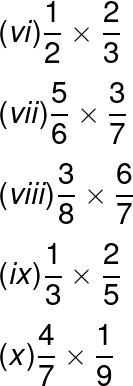


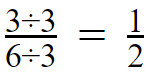
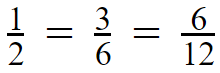
Pingback: Learn Calculating Perimeter of Circle with Equations | Math Tutor
Easy to learn. Thanks.
Pingback: Multiplying Three Fractions | How to Multiply Fractions | Math Tutor
Pingback: Fraction to Decimal and Decimal to Fraction Convert | Math Tutor
Pingback: Representing Data In Pie Chart | Math Tutor