The addition of fractions can discuss in a few categories
- Unit fraction addition
- Improper fraction addition
- Mixed number addition
There is only one golden rule that we have to follow when the adding fractions,
There should be a common denominator between the fractions
Unit Fraction Addition
Example 01:
Like Denominators
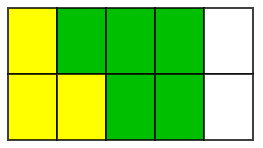
Yellow color area :
Green color area :
Let’s express the shaded area as a fraction,
Here we have a common denominator which is 10.
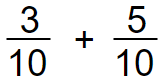
Write the common denominator.
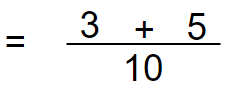
Add the numerators 3 + 5 = 8
In our answer 8 is the numerator and 10 is the denominator. We can also verify the answer by looking at the above figure.
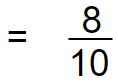
Example 02:
Unlike Denominators
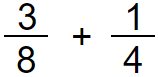
Here we have an unlike denominator, Which means we have a common denominator, So we have to make one.
Denominators are 8 and 4. We can convert 4 into 8 by multiplying 4 by 2.
We have to multiply both numerator and denominator by the same number.
By doing so we will get an equivalent fraction for 1/4 with the denominator 8.
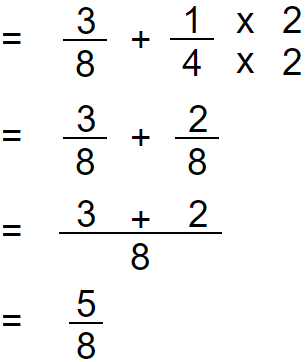
Example 03:
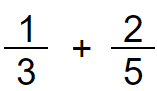
In this example, we have to change both the denominators, because we can’t change 3 to 5 or 5 to 3.
Denominators are 3 and 5. Let’s find the Least Common Multiple (LCM) of 3 and 5.
There are a few methods to find LCM. Here we have mentioned only one way. Here you can learn about other methods of finding LCM.
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33
Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45
LCM is 15.
Our new denominator is 15.
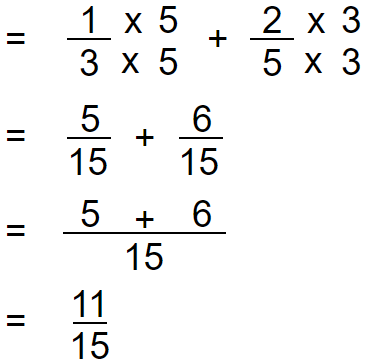
Improper Fraction Addition
Addition of Improper Fractions with Like Denominator
Example 01:
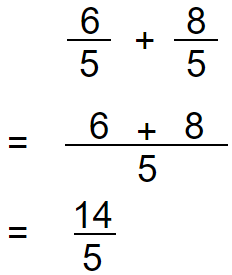
We cannot keep answer as an improper fraction. Convert it into a mixed number.
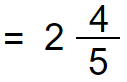
Example 02:
Addition of Improper Fractions with Unlike Denominators
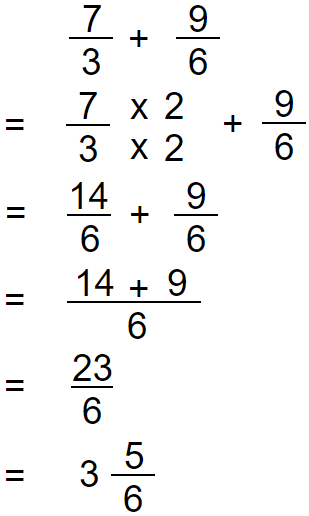
Example 03:
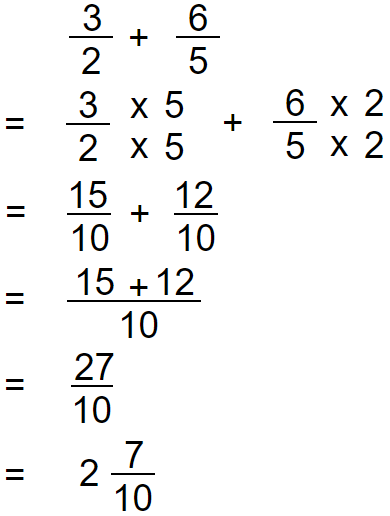
Mixed Number Addition
When we are doing an addition on mixed numbers, first you have to convert the mixed number to an improper fraction.
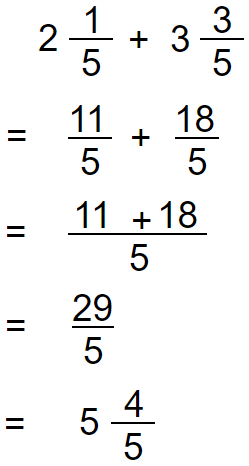
We have another method of adding mixed numbers. Let’s see the same example.
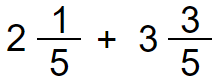
Here we separately add the whole number parts and fractional part and finally join them to take the answer.
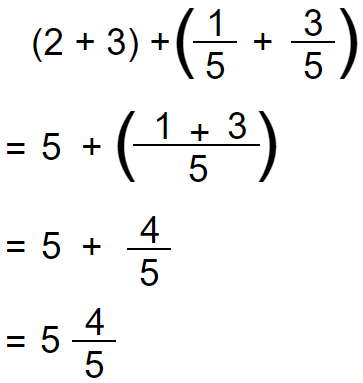


I think addition of fraction is easier to learn and easier to do. What makes is a little difficult and confusing is the process of making different denominators to make it the same and also the additional steps in converting mixed number into improper fraction. If these additional steps are mastered, the learner would no longer have the problem in fraction calculation.